层次分析法(AHP法)是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。
注:
定性:通过非量化的手段来探究事物的本质。
定量:以数量形式存在着的属性,并因此可以对其进行测量。
举个例子:
人物:小强
目的:打算从北京去上海玩
要求:分析他是坐动车去呢?还是坐飞机去呢?还是坐汽车去呢?还是跑过去呢?请根据他个人情况进行最优方案的选择
上述举例的这道题就是一道采用层次分析法来解决的经典题目。现在我们来进行一一分析。
为什么说层次分析法是解决多目标的复杂问题呢?
答:多目标也可以说是多方案。体现在小强从北京去上海玩可以选择不同的出行方案。比如:上面说的坐车,坐火箭,坐航空母舰啥的,或者是走过去。这么多的方案就叫多目标
为什么说是定性和定量相结合呢?
答:定量是对数量形式存在着的属性进行测量的意思。定性则是非数量形式存在着的属性,通过非量化的手段来进行探究。
本题的定性体现在:对于从北京到上海的出行方案肯定要根据小强自身的情况来进行选择。那么所谓的自身情况到底是哪些情况呢?比如经济情况,时间情况,会不会晕车等等。上述这些统称为决定小强出行方案的影响指标,而这些指标到底该选择哪些呢?哪些指标对方案的选择比较大(权重比较大)呢?这就是层次分析法所体现的定性。毕竟这些指标选取得看自身情况来进行主观选择,是没法进行具体的数值量化。
那定量体现在哪里呢?就体现在当小强决定完影响指标有哪些、指标间权重大小到底是多少后,采用层次分析法的具体计算公式进行计算,从而得出最优方案的过程。这就叫做定量。所有层次分析法才说是定性与定量相结合的决策分析方法。
注:权重的意思是哪个指标影响结果更为严重。更为严重的那权重值就大,不严重那权重值就小
根据上述,我们可以知道层次分析法是一种主观的判断方法,因此在数学建模中,不建议单独直接使用。毕竟数学模型讲究的是一个准确性和稳定性。而层次分析法对于指标的选取毕竟是带有主观因素的,怎么选择就有点公说公有理,婆说婆有理的感觉了。所以在比赛中还是慎重使用为好。但并不是说层次分析法不重要哦!!!
现在我们来讲讲层次分析法构造系统模型时的具体步骤。大体上可以分为以下四个步骤:
1. 建立层次结构模型
2. 构造判断(成对比较)矩阵
3. 层次单排序及其一致性检验
4. 层次总排序及其一致性检验
1.建立层次结构模型
首先是需要明确这三点:
决策的目标(你到底要解决什么问题)。eg:小强要从北京去上海,要解决的问题就是用什么方法过去
考虑的因素(决策准则)。eg:影响小强选择去上海的方案的影响因素有哪些?
决策对象。eg:从北京去到上海有哪几套出行方案
接下来就是将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为最高层、中间层和最低层,绘出层次结构图
• 最高层:决策的目的、要解决的问题。
• 中间层:考虑的因素、决策的准则。
• 最低层:决策时的备选方案。
2.构造判断(成对比较)矩阵
所谓的构造判断(成对比较)矩阵就是根据所选影响指标的权重大小,列成矩阵的形式。
比如:小强结合自身情况,决定出出行的影响指标为:
晕车程度(X1) 开销程度(X2) 时间耗费情况(X3)
具体权重(W)大小为: 晕车程度(W1:0.5) 开销程度(W2:0.3) 时间耗费情况(W3:0.2)
那么所构建的判断矩阵则为:

注:权重值之和为1,所谓的成对比较的意思是指标间权重值大小的对比。两两比较构建出三行三列的矩阵出来
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Santy等人提出:一致矩阵法,即:
1. 不把所有因素放在一起比较,而是两两相互比较。
2.对此时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。
心理学家认为成对比较的因素不宜超过9个,即每层不要超过9个因素。因此判断矩阵的元素用Santy的1~9标度方法给出:

注意咯,接下来的内容就涉及到线性代数的知识啦!
构建的判断矩阵还应该满足一致性检验。
首先,介绍一下什么是一致阵?
满足:
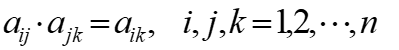
的正互反阵A称一致阵
一致阵的性质:
A的秩为1,A的唯一非零特征根为n
非零特征根n所对应的特征向量归一化后可作为权向量
注:一致性检验并不是说这个矩阵一定要是个一致阵。允许矩阵不一致,但要确定不一致的允许范围,在这个允许的范围内就说明通过了一致性检验,否则不通过的话需要重新的构建这个判断矩阵,改变影响指标的权重和个数,直到满足一致性检验的要求。
对于不一致(但在允许范围内)的成对比较阵A,Saaty等人建议用对应于最大特征根$\lambda$的特征向量作为权向量$\omega$,即:A$\omega$=$\lambda$$\omega$
3.层次单排序及其一致性检验。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。 W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
现在引入线性代数的两个定理:
定理1:$n$ 阶一致阵的唯一非零特征根为n
定理2:$n$ 阶正互反阵A的最大特征根$\lambda\geq n$, 当且仅当$\lambda=n$时A为一致阵
由于λ 连续的依赖于aij,则$\lambda$比$n$ 大的越多,A 的不一致性越严重。用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。因而可以用 λ-n 数值的大小来衡量 A 的不一致程度。
定义一致性指标:$CI=\frac{\lambda-n}{n-1}$。其中:
$CI$=0,有完全的一致性
$CI$接近于0,有满意的一致性
$CI$ 越大,不一致越严重
为衡量CI 的大小,引入随机一致性指标 RI。具体方法步骤为:
1.随机构造500个成对比较矩阵:$A_1,A_2,…,A_500$
2.然后将分别带入带入公式:$CI=\frac{\lambda-n}{n-1}$则可得一致性指标:$CI_1,CI_2,…,CI_500$
从而定义一致性比率 :$CR=\frac{CI}{RI}$
3.一般,当一致性比率$CR=\frac{CI}{RI}$<0.1时,认为A的不一致程度在容许范围之内,有满意的一致性,通过一致性检验。可用其归一化特征向量作为权向量,否则要重新构造成对比较矩阵A,对 $a_\ij$ 加以调整。
4.层次总排序及其一致性检验
•计算某一层次所有因素对于最高层(总目标)相对重要性的权值,称为层次总排序。
•这一过程是从最高层次到最低层次依次进行的。
由于影响指标可能还可以继续细分,如评价一个国家脆弱性(2018年美赛E题第一大题)可以从政治,军事,经济,文化等大方向的影响指标细分到下一级,如:经济可细分为GDP增量,财政收入,人均消费指数等等,因此需要进行多次的层次单排序及其一致性检验。
当$CR<0.1$时,认为层次总排序通过一致性检验。层次总排序具有满意的一致性,否则需要重新调整那些一致性比率高的判断矩阵的元素取值。
到此,根据最下层(决策层)的层次总排序做出最后决策
所以综上所述:人们在对社会、经济以及管理领域的问题进行系统分析时,面临的经常是一个由相互关联、相互制约的众多因素构成的复杂系统。层次分析法则为研究这类复杂的系统,提供了一种新的、简洁的、实用的决策方法。
层次分析法的优点:
1.系统性:将对象视作系统,按照分解、比较、判断、综合的思维方式进行决策。成为成为继机理分析、统计分析之后发展起来的系统分析的重要工具;
2.实用性:定性与定量相结合,能处理许多用传统的最优化技术无法着手的实际问题,应用范围很广,同时,这种方法使得决策者与决策分析者能够相互沟通,决策者甚至可以直接应用它,这就增加了决策的有效性;
3.简洁性:计算简便,结果明确,具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤,容易被决策者了解和掌握。便于决策者直接了解和掌握。
层次分析法的局限:
1.囿旧:只能从原有的方案中优选一个出来,没有办法得出更好的新方案;
2.粗略:该法中的比较、判断以及结果的计算过程都是粗糙的,不适用于精度较高的问题;
3.主观:从建立层次结构模型到给出成对比较矩阵,人主观因素对整个过程的影响很大,这就使得结果难以让所有的决策者接受。当然采取专家群体判断的办法是克服这个缺点的一种途径。

