浅谈BP神经网络的原理

2020-02-19

神经网络的工作状态分为学习和工作两种状态

学习：利用学习算法来调整神经元间的连接权重，使得网络输出更符合实际

工作：神经元间的连接权值不变，可以作为分类器或者预测数据之用。

采用BP学习算法的前馈神经网络称为BP神经网络。

BP算法基本原理：利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差，如此一层一层的反传下去，就获得了所有其他各层的误差估计。

特点：信号的正向传播&误差的反向传播

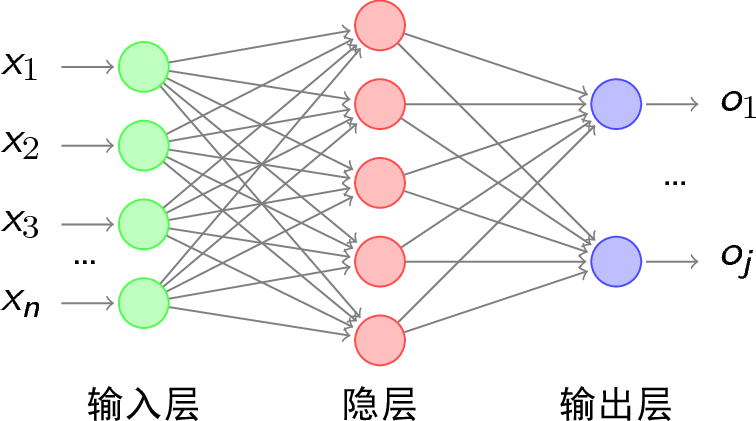
BP神经网络的结构一般分为三层，即：输入层，隐含层，输出层，如上图所示。

一般神经网络的神经元个数设置为：隐含层$\geq\sqrt{输入层+输出层}$

在该神经网络中，其基本单位（基本元素）为神经元。作为神经网络的基本元素，神经元的模型如下所示：

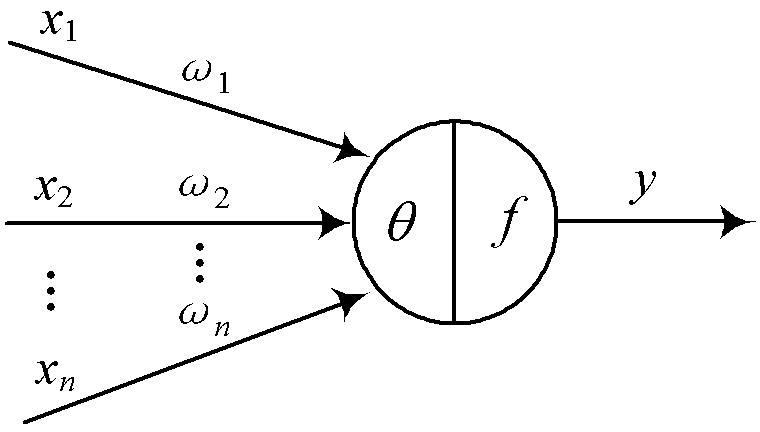
其中：$X_1$~$X_n$是从其他神经元传来的输入信号；$W_1$~$W_n$表示神经元之间的连接权值；θ表示一个阈值 ( threshold )，或称为偏置( bias )。

注：$W_{ij}$表示表示从神经元$j$到神经元$i$的连接权值

激活函数是对净激活量与输出进行映射的函数。一些常用的激活函数,由于输入数据与期望值之间可能并不是量级一样，所以需要激活。

激活函数主要有以下几种：

其中S形和双极S形函数图像为：

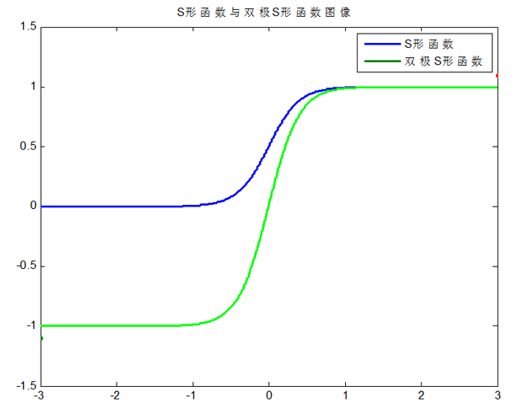
由上图可知：S形和双极S形函数均为连续函数（其导函数也均为连续函数）。唯一的不同之处在于：$f(x)$区间值的不同，S形函数的区间在0~1；双极S形函数的区间在-1~1

根据网络中神经元的互联方式的不同，网络模型分为：

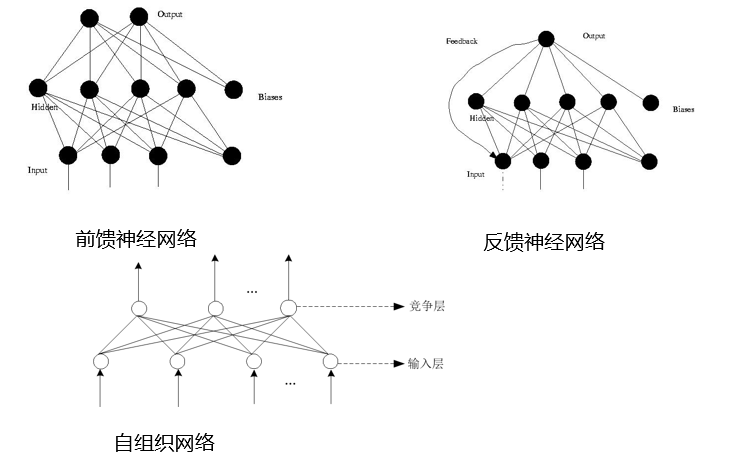
前馈神经网络

只在训练过程会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层，层间没有向后的反馈信号

反馈神经网络

从输出到输入具有反馈连接的神经网络，其结构比前馈网络要复杂得多

自组织网络

通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数与结构。

假设输入层有n个神经元，隐含层有p个神经元，输出层有q个神经元

符号定义

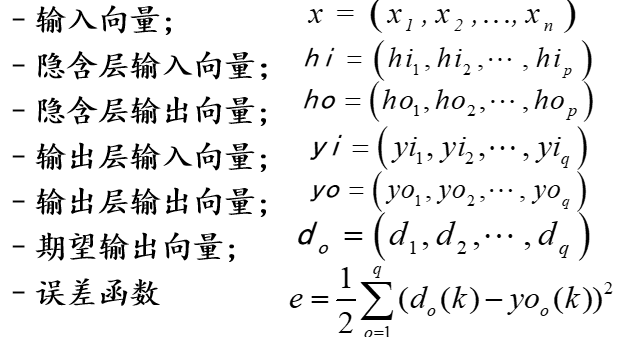
具体步骤：

首先，计算各层神经元的输入和输出

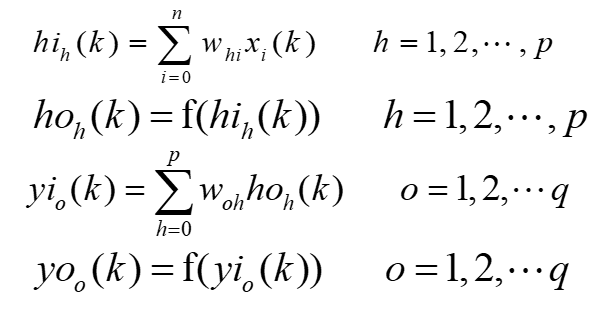
第二步：利用网络期望输出和实际输出，计算误差函数对输出层的各神经元的偏导数。

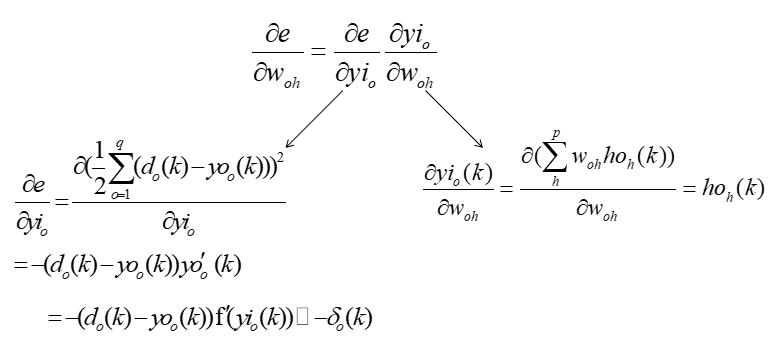
第三步：利用隐含层到输出层的连接权值、输出层的$\delta{_0(k)}$和隐含层的输出计算误差函数对隐含层各神经元的偏导数$\delta{_h(k)}$ 。

第四步，利用输出层各神经元的$\delta{0(k)}$和隐含层各神经元的$\omega{{oh}(k)}$输出来修正连接权值。

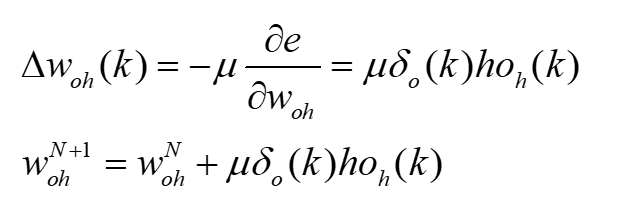
注：$\mu$是设置的学习率。

第五步，利用隐含层各神经元的$\delta{_h(k)}$和输入层各神经元的输入修正连接权。

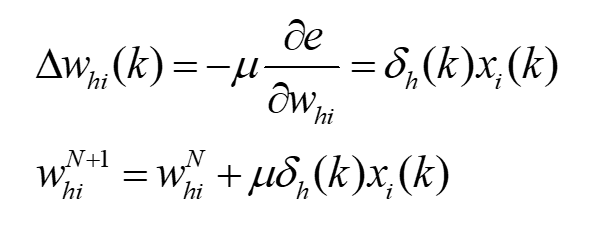
第六步，计算全局误差

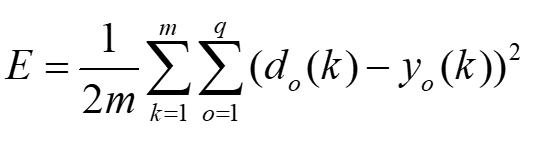
第七步，判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，返回进入下一轮学习。

BP网络的训练就是通过应用误差反传原理不断调整网络权值使网络模型输出值与已知的训练样本输出值之间的误差平方和达到最小或小于某一期望值。虽然理论上早已经证明：具有1个隐层（采用Sigmoid转换函数）的BP网络可实现对任意函数的任意逼近。但遗憾的是，迄今为止还没有构造性结论，即在给定有限个（训练）样本的情况下，如何设计一个合理的BP网络模型并通过向所给的有限个样本的学习（训练）来满意地逼近样本所蕴含的规律（函数关系，不仅仅是使训练样本的误差达到很小）的问题，目前在很大程度上还需要依靠经验知识和设计者的经验。因此，通过训练样本的学习（训练）建立合理的BP神经网络模型的过程，在国外被称为“艺术创造的过程”，是一个复杂而又十分烦琐和困难的过程。

由于BP网络采用误差反传算法，其实质是一个无约束的非线性最优化计算过程，在网络结构较大时不仅计算时间长，而且很容易限入局部极小点而得不到最优结果。目前虽已有改进BP法、遗传算法（GA）和模拟退火算法等多种优化方法用于BP网络的训练(这些方法从原理上讲可通过调整某些参数求得全局极小点)，但在应用中，这些参数的调整往往因问题不同而异，较难求得全局极小点。这些方法中应用最广的是增加了冲量（动量）项的改进BP算法。

学习率和冲量系数

学习率影响系统学习过程的稳定性。大的学习率可能使网络权值每一次的修正量过大，甚至会导致权值在修正过程中超出某个误差的极小值呈不规则跳跃而不收敛；但过小的学习率导致学习时间过长，不过能保证收敛于某个极小值。所以，一般倾向选取较小的学习率以保证学习过程的收敛性（稳定性），通常在0.01~0.8之间。
增加冲量项的目的是为了避免网络训练陷于较浅的局部极小点。理论上其值大小应与权值修正量的大小有关，但实际应用中一般取常量。通常在0~1之间，而且一般比学习率要大。

Matlab包含的训练函数：

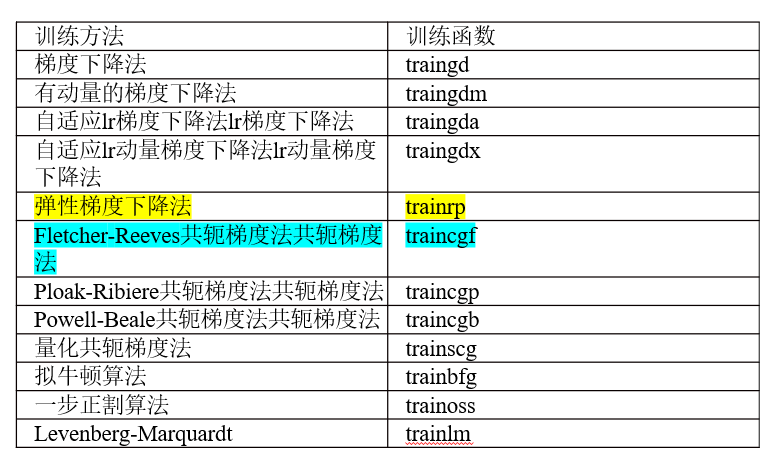
Matlab中BP神经网络的封装函数介绍：

（1）生成BP网络

1	net=newff(PR,[S1 S2...SNl]),{TF1 TF2...TFNl},BTF)

PR：由R维的输入样本最小最大值构成的R\2*维矩阵。

[S1 S2…SNl]：各层的神经元个数。

{TF1 TF2…TFNl}：各层的神经元传递函数。

BTF：训练用函数的名称。

（2）网络训练

net=train(net,P,T)

（3）网络仿真

Y2=sim(net,P2)

Matlab中BP神经网络的参考代码：

pn=p1';tn=t1';
[m,n]=size(t);
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);  net=newff(minmax(pn),[5,1],{'tansig','purelin'},'traingd'); %设置网络,建立相应的BP网络
net.trainParam.show=50; % 训练网络
net.trainParam.lr=0.01;
net.trainParam.epochs=1000;
net.trainParam.goal=1e-5;
[net,tr]=train(net ,pn,tn);     
anewn=sim(net,pn);   %对BP网络进行仿真
figure;hold on
plot(anewn,'b',tn,'r');
wucha=sum(abs(b-r))/n;%误差输出

举例1：


clear;
clc;
P=[-1 -1 2 2 4;0 5 0 5 7];
T=[-1 -1 1 1 -1];
%利用minmax函数求输入样本范围
net = newff(minmax(a1),[7,1],{'tansig','purelin'},'trainlm');
net.trainParam.show=50;%
net.trainParam.lr=0.05;
net.trainParam.epochs=1000;
net.trainParam.goal=1e-5;
[net,tr]=train(net,a1,a2);
net.iw{1,1}%隐层权值
net.b{1}%隐层阈值
net.lw{2,1}%输出层权值
net.b{2}%输出层阈值`
y3=sim(net,a1);

举例2：

clear;
clc;
X1=-1:0.1:1；
X2=0.1:1:2;
D=[-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609...
0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 -.0988...
0.3072 0.3960 0.3449 0.1816 -0.312 -0.2189 -0.3201];
x3=[0.5;3]
figure;
plot(X,D,'*'); %绘制原始数据分布图
net = newff([-1 1],[5 1],{'tansig','tansig'});
net.trainParam.epochs = 100; %训练的最大次数
net.trainParam.goal = 0.005; %全局最小误差
net = train(net,X,D);
O = sim(net,X);
figure;
plot(X,D,X,O,'r'); %绘制训练后得到的结果和误差曲线
V = net.iw{1,1}%输入层到中间层权值
theta1 = net.b{1}%中间层各神经元阈值
W = net.lw{2,1}%中间层到输出层权值
theta2 = net.b{2}%输出层各神经元阈值