浅谈数据结构排序算法中的希尔排序

2020-02-27

数据结构中的排序算法有：插入类排序、交换类排序、选择排序、堆排序、归并排序、桶排序。而插入类排序包括：直接插入排序、折半插入排序、希尔排序。

其中：希尔排序（不稳定的排序）

希尔排序又称：缩小增量排序。什么是不稳定的排序呢？意思是假如未排序前的序列存在两个值相同的元素，经过希尔排序后，这两个值在排完的有序序列中的先后位置会发生改变。反之，稳定的排序则不会发生改变。

为什么希尔排序是不稳定的排序呢？因为：不同的增量可能把相同的关键字划分到两个子序列中执行直接插入排序。

希尔排序可以理解为：要对整个班级按照身高从低到高排列。希尔排序就是首先将班级人数分成5排，然后对每一列进行排序；当排序完后再将队伍分成2排，再次对每一列的同学进行身高排序；当再次排序完后最后队伍分成1排，对每一列的同学进行身高排序（此时就是简单的插入排序了）。

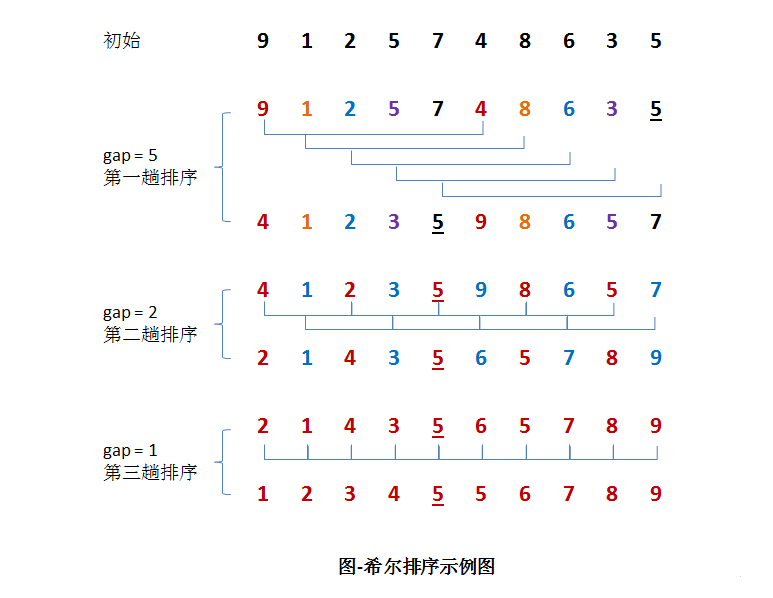
注：下列两种方法都是从小到大排序

方法一：建立哨兵（A[0]为哨兵，类似于中介变量，用于暂存元素值）

#include <iostream>
using namespace std;//调用命名空间std内定义的所有标识符
#define  ElemType int
ElemType A[] = { 8,9,1,2,5,7,4,8,6,3,5};//定义要排序的数组
int n = 10;//从A[1]-A[n]。A[0]当哨兵，用于暂存元素值，其初始元素值不算在要排序的序列中
void ShellSort(ElemType A[], int n)
{
	int i, j, d;
	for(d=n/2;d>=1;d=d/2)//每次增量大小对半切（缩小增量），d=d/2（向下取整），最后一次d取到1，所以限制条件d>=1
		for(i=d+1;i<=n;i++)////i=d+1和i<=n：加一是为了扣除A[0]，如果采用temp存储则要改成i=d和i<n。区间内元素的比较次数，增量越小，比较次数越多
			if(A[i]<A[i-d])//相差d的元素进行对比，因为是从小到大排序，所以如果后面的元素比前面的大，那就要对换两个元素的位置
			{
				A[0] = A[i];//用于暂存作用
				for (j = i - d;j > 0 && A[0] < A[j];j -= d)//j > 0:为了排除A[0]，若用temp变量进行暂存，则改为j >= 0&& temp < A[j](见方法二)
					A[j + d] = A[j];//对每个增量区间的对应位置的元素从后向前进行一一比对，不满足A[0] < A[j]或者直到比较完所有区间的对应位置元素后，跳出for循环 
				A[j + d] = A[0];//将值插入
			}
}
int main()
{
	ShellSort(A, n);//调用希尔排序算法
	cout << "数组A[]的最终排序为：";
	for (int x = 1;x <=n;x++)
		cout << A[x] << "  ";	
}

ShellSort的复杂度分析非常复杂，不同gap序列的设计对应不同的复杂度。

最坏时间复杂度：根据步长序列的不同而不同。已知最好的： O($n (logn) ^2$)
最优时间复杂度: O($n$)
平均时间复杂度：根据步长序列的不同而不同。
最坏空间复杂度：O($n^2$)（增量元素不互质，小增量可能根本不起作用）

空间复杂度：O(1) 注：哨兵A[0]（常数个空间）

方法二：设定一个中间变量temp（主流）

#include <iostream>
using namespace std;//调用命名空间std内定义的所有标识符
#define  ElemType int
ElemType A[] = { 8,9,1,2,5,7,4,8,6,3,5 };//定义要排序的数组
int n = 10;//n=size(A)
void ShellSort(ElemType A[], int n)
{
	int i, j, d,temp;
	for (d = n / 2;d >= 1;d = d / 2)//每次增量大小对半切（缩小增量），d=d/2（向下取整），最后一次d取到1，所以限制条件d>=1
		for (i = d ;i <n;i++)//区间内元素的比较次数，增量越小，比较次数越多
			if (A[i] < A[i - d])//相差d的元素进行对比，因为是从小到大排序，所以如果后面的元素比前面的大，那就要对换两个元素的位置
			{
				temp = A[i];//用于暂存作用
				for (j = i - d;j >=0 &&temp < A[j];j -= d)
					A[j + d] = A[j];//对每个增量区间的对应位置的元素从后向前进行一一比对，不满足A[0] < A[j]或者直到比较完所有区间的对应位置元素后，跳出for循环 
				A[j + d] = temp;//将值插入
			}
}


int main()
{
	ShellSort(A, n);//调用希尔排序算法
	cout << "数组A[]的最终排序为：";
	for (int x = 0;x <n;x++)
		cout << A[x] << "  ";	
}

空间复杂度：O(1) 注：中间变量temp（常数个空间）`

步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，直到最终算法以步长为1进行排序。

Donald Shell最初建议步长选择为 n/2 并且对步长取半直到步长达到1。虽然这样取可以比 O(n^2)类的算法更好，但这样仍然有减少平均时间和最差时间的余地。

已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,…)。这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。”用这样步长序列的希尔排序比插入排序要快，甚至在小数组中比快速排序和堆排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

另一个在大数组中表现优异的步长序列是（斐波那契数列除去0和1将剩余的数以黄金分区比的两倍的幂进行运算得到的数列）：(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713,…)